1. 관점(1): 소개

   선형대수학에서는 하나의 대상을 여러 가지 관점에서 바라봅니다. <프롤로그(1): 벡터>에서 언급했던 것처럼 다항식, 함수, 수열 등을 벡터로 보기도 하고, <프롤로그(2): 행렬>에서 언급했던 것처럼 연립일차방정식을 행렬로 보기도 합니다. 이번 글에서는 후자의 주제를 좀 더 확장하여 선형대수학에서 연립일차방정식

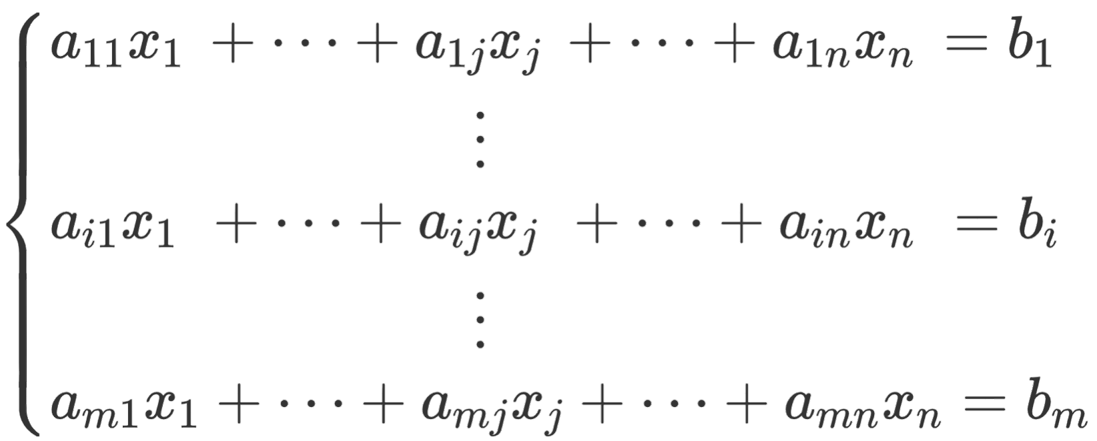
을 보는 여러 관점에 대해 소개합니다.

첨가행렬

   '첨가행렬(augmented matrix)'이란 연립일차방정식에서 미지수, 덧셈 기호, 등호 등을 생략하여

$\left[ \begin{array}{ccccc|c}\,\,a_{11}\,\,&\cdots&\,\,a_{1j}\,\,&\cdots&\,\,a_{1n}\,\,&\,b_1\,\\\vdots&&\vdots&&\vdots&\vdots\\\,\,a_{i1}\,\,&\cdots&\,\,a_{ij}\,\,&\cdots&\,\,a_{in}\,\,&\,b_i\,\\\vdots&&\vdots&&\vdots&\vdots\\\,\,a_{m1}\,\,&\cdots&\,\,a_{mj}\,\,&\cdots&\,\,a_{mn}\,\,&\,b_m\,\end{array} \right]$

와 같이 계수(coefficient)와 상수항(constant)으로 구성한 행렬을 말합니다. 계수만으로 이루어진 계수행렬(coefficient matrix)

$\left[ \begin{array}{ccccc}\,\,a_{11}\,\,&\cdots&\,\,a_{1j}\,\,&\cdots&\,\,a_{1n}\,\,\\\vdots&&\vdots&&\vdots\\\,\,a_{i1}\,\,&\cdots&\,\,a_{ij}\,\,&\cdots&\,\,a_{in}\,\,\\\vdots&&\vdots&&\vdots\\\,\,a_{m1}\,\,&\cdots&\,\,a_{mj}\,\,&\cdots&\,\,a_{mn}\,\,\end{array} \right]$

에 상수항으로 이루어진 열이 '첨가'된 것이라 하여 '첨가행렬', '붙임행렬', 또는 '덧붙인 행렬' 등으로 불립니다. (첨가행렬 맨 오른쪽 열의 왼쪽에 수직으로 그은 선은 계수 부분과 상수 부분을 구분하기 위한 것으로, 생략할 수 있습니다.) 연립일차방정식의 풀이법인 '가우스 소거법(Gaussian elimination)'을 행렬의 형태로 이해하고자 할 때 사용되는 표기법입니다.

행렬방정식

   행렬의 곱을 이용하면, 연립일차방정식을 다음과 같이 표기할 수 있습니다. 

$\begin{bmatrix}a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\\vdots&&\vdots&&\vdots\\a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\\vdots&&\vdots&&\vdots\\a_{m1}&\cdots&a_{mj}&\cdots&a_{mn}\end{bmatrix}\begin{bmatrix}x_1\\[5pt]\vdots\\[5pt]x_j\\[5pt]\vdots\\[5pt]x_n\end{bmatrix}=\begin{bmatrix}b_1\\\vdots\\b_i\\\vdots\\b_m\end{bmatrix}$

이때, 행렬 $A$를

$A=\begin{bmatrix}a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\\vdots&&\vdots&&\vdots\\a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\\vdots&&\vdots&&\vdots\\a_{m1}&\cdots&a_{mj}&\cdots&a_{mn}\end{bmatrix}$

로 정의하고, 두 벡터 $\mathbf{x}$와 $\mathbf{b}$를 각각

$\mathbf{x}=\begin{bmatrix}x_1\\[5pt]\vdots\\[5pt]x_j\\[5pt]\vdots\\[5pt]x_n\end{bmatrix}$와 $\mathbf{b}=\begin{bmatrix}b_1\\\vdots\\b_i\\\vdots\\b_m\end{bmatrix}$

로 정의하면, 위의 연립일차방정식은

$$\bbox[#FFFFCC,1pt]{A\mathbf{x}=\mathbf{b}}$$

와 같은 형태로 나타낼 수 있는데, 이 같은 방정식을 '행렬방정식(matrix equation)'이라고 합니다. (참고로 $A$는 계수(coefficient)만으로 이루어진 '계수행렬(coefficient matrix)'입니다.)

벡터방정식

   연립일차방정식을 나타내는 또 다른 방법은 계수행렬 $A$를 열벡터(column vector)로 쪼개어 보는 것인데, $j=1, \cdots, n$에 대하여 $A$의 $j$번째 열을 $\mathbf{a}_j$로 나타내기로 하면, $A\mathbf{x}$는

$$\begin{align}&\quad\,\,\begin{bmatrix}a_{11}{\color{#ee2323}x_1}+\cdots+a_{1j}{\color{#ee2323}x_j}+\cdots+a_{1n}{\color{#ee2323}x_n}\\\vdots\\a_{i1}{\color{#ee2323}x_1}+\cdots+a_{ij}{\color{#ee2323}x_j}+\cdots+a_{in}{\color{#ee2323}x_n}\\\vdots\\a_{m1}{\color{#ee2323}x_1}+\cdots+a_{mj}{\color{#ee2323}x_j}+\cdots+a_{mn}{\color{#ee2323}x_n}\end{bmatrix}\\[5pt] &=\begin{bmatrix}a_{11}{\color{#ee2323}x_1}\\\vdots\\a_{i1}{\color{#ee2323}x_1}\\\vdots\\a_{m1}{\color{#ee2323}x_1}\end{bmatrix}+\cdots+\begin{bmatrix}a_{1j}{\color{#ee2323}x_j}\\\vdots\\a_{ij}{\color{#ee2323}x_j}\\\vdots\\a_{mj}{\color{#ee2323}x_j}\end{bmatrix}+\cdots+\begin{bmatrix}a_{1n}{\color{#ee2323}x_n}\\\vdots\\a_{in}{\color{#ee2323}x_n}\\\vdots\\a_{mn}{\color{#ee2323}x_n}\end{bmatrix}\\[5pt]&={\color{#ee2323}x_1}\begin{bmatrix}a_{11}\\\vdots\\a_{i1}\\\vdots\\a_{m1}\end{bmatrix}+\cdots+{\color{#ee2323}x_j}\begin{bmatrix}a_{1j}\\\vdots\\a_{ij}\\\vdots\\a_{mj}\end{bmatrix}+\cdots+{\color{#ee2323}x_n}\begin{bmatrix}a_{1n}\\\vdots\\a_{in}\\\vdots\\a_{mn}\end{bmatrix}\\[7pt]&={\color{#ee2323}x_1}\mathbf{a}_1+\cdots+{\color{#ee2323}x_j}\mathbf{a}_j+\cdots+{\color{#ee2323}x_n}\mathbf{a}_n\end{align}$$

와 같이 나타낼 수 있습니다. 따라서 기존의 연립일차방정식은

$$\bbox[#FFFFCC,1pt]{x_1\mathbf{a}_1+\cdots+x_j\mathbf{a}_j+\cdots+x_n\mathbf{a}_n=\mathbf{b}}$$

처럼 표기할 수 있죠. 이는 벡터를 포함한 방정식이므로 '벡터방정식(vector equation)'이라고 합니다.

선형변환

   이번에는 지금까지보다 더 색다른 접근법으로 연립일차방정식(또는 행렬방정식)의 좌변을

$$\mathbf{x} \longmapsto A\mathbf{x}$$

인 함수로 생각합니다. 보다 구체적으로 말하면 $\mathbb{R}^n$에서 $\mathbb{R}^m$으로의 함수 $T$를

$$T(\mathbf{x})=A\mathbf{x}$$

로 정의하는 것이죠. 그러면 연립일차방정식이 물어보는 것은

$\mathbb{R}^m$의 원소 $\mathbf{b}$에 대하여,
함수 $T$에 의해 $\mathbf{b}$와 대응되는
정의역 $\mathbb{R}^n$의 원소 $\mathbf{x}$는 무엇인가?

가 됩니다. 이때 중요한 것은 함수 $T$가 '선형변환(linear transformation)'이라는 것입니다. 선형변환이란 함수의 일종으로, 정의역의 임의의 원소 $\mathbf{u}, \mathbf{v}$와 임의의 스칼라 $c$에 대하여

$$\bbox[#FFFFCC,1pt]{T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})}$$

$$\bbox[#FFFFCC,1pt]{T(c\mathbf{u})=cT(\mathbf{u})}$$

가 성립하는 함수를 말합니다. (선형변환을 일반적으로 $T$로 표기하는데, 이는 'transformation'의 앞 글자를 딴 것입니다.)

   위에서 정의한 함수 $T$의 경우, 임의의 $\mathbf{u}=(u_1, \cdots, u_n)$, $\mathbf{v}=(v_1, \cdots, v_n) \in \mathbb{R}^n$와 $c \in \mathbb{R}$에 대하여

$$\begin{align}T(\mathbf{u}+\mathbf{v})&=A(\mathbf{u}+\mathbf{v})\\[5pt]&=(u_1+v_1)\mathbf{a}_1+\cdots+(u_n+v_n)\mathbf{a}_n\\[5pt]&=(u_1\mathbf{a}_1+\cdots+u_n\mathbf{a}_n)\\[4pt]&\quad \,+(v_1\mathbf{a}_1+\cdots+v_n\mathbf{a}_n)\\[5pt]&=A\mathbf{u}+A\mathbf{v}\\[5pt]&=T(\mathbf{u})+T(\mathbf{v})\end{align}$$

이고,

$$\begin{align}T(c\mathbf{u})&=A(c\mathbf{u})\\[5pt]&=(cu_1)\mathbf{a}_1+\cdots+(cu_n)\mathbf{a}_n\\[5pt]&=c(u_1\mathbf{a}_1)+\cdots+c(u_n\mathbf{a}_n)\\[5pt]&=c(u_1\mathbf{a}_1+\cdots+u_n\mathbf{a}_n)\\[5pt]&=c(A\mathbf{u})\\[5pt]&=cT(\mathbf{u})\end{align}$$

이므로, 함수 $T$는 선형변환입니다. (간단히 말해서, $\mathbf{x} \mapsto A\mathbf{x}$인 함수는 모두 선형변환입니다.)

   여기까지 연립일차방정식을 바라보는 관점을 크게 네 가지

첨가행렬
행렬방정식
벡터방정식
선형변환

로 정리했습니다. 앞으로는 이러한 관점에서 연립일차방정식에 접근하며, 연립일차방정식에서 일어나는 일들이 각각의 관점에서는 어떤 모습으로 나타나는지를 살펴봅니다.